Determination of the heat transfer coefficient $\mathbf h$ in a cooling tube

A.Hormière, ST-CV, 17/08/2001

Back

Abstract:

This document gives the details of the determination of the heat transfert coefficient in a cooling tube. It allows the calculation of the temperature difference between the mean water temperature $T_m$ and the inside surface temperature of the pipe $T_s$.

Introduction

When the water flows in a cooling tube, a thermal boundary layer is developing. There is a temperature gradient between the internal surface of the pipe and the water to allow heat transfer. There is also a gradient inside the water (Figure 1).
It is very difficult to know precisely the temperature gradient inside the water, for this reason, we use the mean temperature value $T_m$, which is the averaged value of the temperature at a position x.
The heat transfer coefficient $h$ between $T_m$ and the inside surface temperature $T_s$ can be evaluated using correlations on the Nusselt Number ($Nu$) which represent the ration between convection and conduction heat transfer.
As we know $h$, we can evaluate the temperature difference between $T_m$ and $T_s$ for a certain heat flux $\phi$.

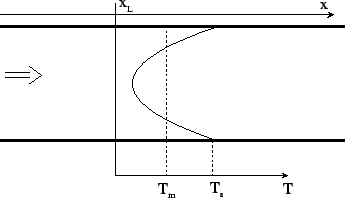
Figure1: Temperature gradient in a cooling pipe $T_s > T_m$, at $x=x_L$

Correlations

Lets consider a tube of internal diameter $D$, with a fluid flow of speed $U$. The fluid is characterized by its density $\rho$, thermal capacity $C_p$, thermal conductivity $\lambda$ and dynamic viscosity $\mu$.
The Nusselt number is adimensional and defined as: $Nu=\frac{h \, D}{\lambda}$. As we know $Nu$, we can determine $h$.

In this type of flow, $Nu$ is a constant for laminar flow and a fonction of two other adimensional numbers, $Pr$ and $Re$, $Nu=Nu(Re,Pr)$ for turbulent flows. $Pr$ depends only of the fluid used, it is defined as $Pr=\frac{\nu}{a}$ wher $\nu$ is the kinematic viscosity $\nu=\frac{\mu}{\rho}$ and $a$ the thermal diffusivity $a=\frac{\lambda}{\rho \, C_p}$. For the water $Pr \simeq 7.5$. $Re$ depends on the fluid an the motion conditions, $Re=\frac{U \, d}{\nu}$.

We use the Dittus-Boelter equation from [1] for turbulent flow ($Re>10^4$) and the value 4.36 for laminar flow ($Re < 2500$). Between this range, we assume a linear behavior to cover the whole range of flows. The equation is valid after a certain length of pipe, typically 10$D$.
The following equation is only valid for water, as we need to fix a $Pr$ to make the linear approximation. It can easily be extended to another type of fluid.

$$\boxed { Nu= \begin {cases} 4.36& \text{if $Re < 2500$} \\ \... ...Re^\frac{4}{5} \, Pr^{0.4}& \text{if $Re>10^4$\ and $0.7<Pr<160$} \end{cases}}$$

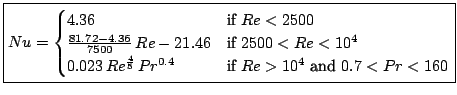
When we have the $Nu$, we apply: $h=\frac{Nu \, \lambda}{D}$.

In the Figure 2 we can see that $Nu$ increases with $Re$, which means for a pipe of a diameter $D$, $Nu$ ie $h$ increases with the speed $U$.

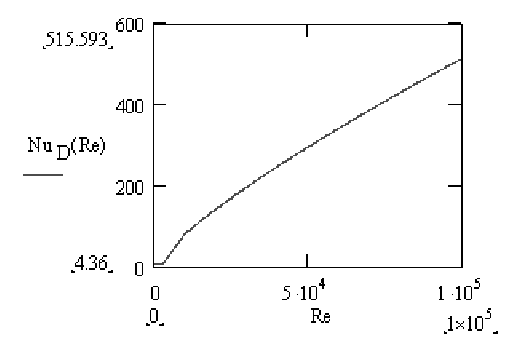
Figure2: Nusselt number fonction of Reynolds for a water cooling pipe

Top

Bibliography

 

1

Franck P. Incropera and David P. DeWitt.
Fundamentals of Heat and Mass Transfer.
John Wiley & Sons, 1996.