Heat transfert calculation in a tube

Back

Abstract:

This document gives the details of a heat transfert calculation in an insulated tube to find the temperature rising.

Let's consider a pipe like in the figure below. We apply the conservation of energy on the volume. The heat that enters the volume is $\dot{H_1}$ with $\dot{H_1} = \dot{m}C_p T_1$ where $\dot{m}$ is the mass flow rate and $C_p$ the heat capacity.
$\phi$ is the heat flux on the tube from the outside, by length of the tube ($W/m$).

 

Figure: Heat exchange on a pipe chunk

 

The conservation of the energy gives us:

$$\dot{H_2}=\dot{H_1}+ \phi \,dx$$

That gives:

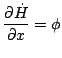$$\frac{\partial \dot{H}}{\partial x} =\phi$$ (1)

We have now to define the heat flux $\phi$ per meter of tube. We only have to make a bi-dimensional analyse on a section of the tube.

Figure: Section of an insulated pipe

The parameters are $T_{in}$ the temperature of the fluid in this section. We suppose that the wall of the tube is at the same temperature (thickness neglected). $T_{ext}$ the temperature of the ambient. $r_1$ and $r_2$, respectively the external radius of the tube and the radius of the tube with insulation. $\lambda$ is the heat conduction coefficient of the insulation and $h$ the global heat exchange coefficient with the ambient (convection + radiations).
We can write:

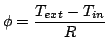$$\phi = \frac {T_{ext} - T_{in}} {R}$$ (2)

With $R$ the global resistance of the air and the insulation.

$R= \frac {\ln \left( r_2/r_1 \right) } {2 \pi \lambda} + \frac {1} {h \, 2 \pi r_2}$

From (1) , (2) and the definition of $\dot{H}$, we can write:

$$\frac {\partial T}{\partial x} = \frac {-\left( T(x) - T_{ext} \right)} {\dot{m} C_p \, R}$$

$$\Longleftrightarrow \frac {\partial \theta}{\partial x} = \frac {-\theta(x)} {\dot{m} C_p \, R}$$

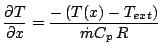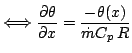That, after some calculations gives:

$$\boxed{ T(x)= \left( T_{x=0} - T_{ext} \right) \exp^{- \frac {x} {\dot{m} C_p \, R} } + T_{ext} }$$

top