A. Hormière ST-CV
2002-01-22

 Back

---

 => Introduction

=> Position of the problem

=> Model

=> Results

=> Conclusion

---

  

Introduction

 In the cooling plant of ECAL, an immersion heater is foreseen to ensure a fast and precise regulation. It is important to understand well the behaviour of this heater, especially its transient state.

  

Position of the problem

 A resistance is inserted in the pipe; when the temperature needs to be increased, a current is sent through this resistance. The heat is released by Joule effect in the resistance. However, this heat isn’t dissipated immediately in the fluid. A temperature difference between the heater and the water is needed to allow heat transfer. One part of the heat will increase the heater, until a sufficient temperature difference is reached. We are interested in reducing the transient time.

  

Model

We use the following Model:

 

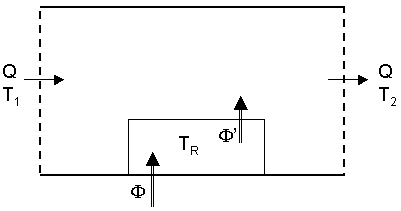
A flow rate Q (kg/s) passes through the pipe. The inlet temperature is T₁, and the outlet temperature T₂. A known heat flow F (W) is generated inside the resistance, while F’ is dissipated from the resistance to the water. T_R is the temperature of the resistance.

 

We will use:

Cp_w: the specific heat of the fluid in motion 
M_R and Cp_R: respectively the mass and the specific heat of the resistance
S and h: the surface between the fluid and the resistance and the convection coefficient

 

We have the following relations:

 

Assuming T₁ and F constant, the solution is:

with            

 

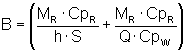
 In a steady state, F’=F, which gives straightforward T_R and T₂.

  

Results

 The outlet temperature changes exponentially. The transient time is directly linked to the coefficient B. It has to be as small as possible to give the shortest transient.

 If we take the example of the immersion heater needed for a Super Module:

 S~0.08 m², h[i]~3000 S.I., Cp_W~4000 S.I. and Q~2 kg/s.

 The second term of B can be neglected compared to the first one. To minimize the transient time, has to be minimized.

Some graph and the example above are available in a Mathcad calculation page (link, file), where it is obvious that in our case, the flow rate doesn't directly influence the transient duration (even if it has an influence in the value of h). 

 Conclusion

 The choice of the heater has to be done by maximizing the heat transfer (h), the surface between the resistance and the fluid (S) and minimizing the specific heat and the mass of the resistance (Cp_R and M_R). This would guaranty a minimum transient time.

 

---